Helping a child with dyscalculia to learn their maths facts
This post describes the system that I use with my dyscalculic child for learning maths facts. At the point of beginning this system, my child knew almost no maths facts at all, and was struggling to retain even +1 facts. These strategies have enable them to learn all addition facts to 20 and subtraction facts to 10. We are now successfully working on subtraction facts to 20 and multiplication. It’s been a game changer for us!
Why focus on basic maths facts?
Dyscalculia is often associated with working memory deficits, which makes it especially important for children to have quick recall of their basic facts. If they are sure of their basic facts, the child will not have to use up valuable working memory capacity figuring out those facts as part of a larger equation. In my experience, my child can also easily become confused whilst working on mathematics, especially word problems. I want them to be really confident and solid in their basic facts, so that they can focus on reasoning through the maths problem, and not lose sight of the bigger picture.

I am not encouraging ‘memorisation’ in the typical sense, but rather the development of strategies that enable the quick ongoing recall of these facts. My child is able to rote learn some facts, but these will just slip out of their head when other facts are added. What is needed is deep conceptual understanding, and a visual strategy for bring the answer to mind. We use a range of strategies, some from the wonderful Ronit Bird, some from our maths curriculum (Math with Confidence), and some we have made up!
Spaced repetition
Spaced repetition is an evidence-based system of learning new information. Each new fact is ‘rehearsed’ (checked) at gradually expanding intervals of time. It is probably easiest to explain spaced-repetition through the example of our maths facts box.
I keep an index-card box with our maths supplies, with the address-card organisers turned backwards and relabelled. The categories are:
- Several times daily
- Daily
- Odd/Even days (one card each for odd and even days of the month)
- Days of the Week (one card each for Monday, Tuesday, Wednesday, Thursday, Friday)
- All the days of the month but allocated in pairs 15 days apart (e.g. the first card is 1,16, the second card is 2,17, and so on. I originally wanted to do each day of the month on its own card and ran out, but I actually prefer the once-a-fortnight repetition. I don’t actually use Day 31 because it doesn’t come round often enough).

New facts start at the front of the box. If they are answered correctly and quickly, they move back one category (e.g. from ‘Daily’ to ‘Odd Days’, or from ‘Wednesday’ to ‘Dates 3rd and 18th’. If they are answered correctly but there is a little hesitation, I keep them where they are. If the fact is answered incorrectly, or with lots of hesitation, it goes back to the front of the box.
Thus, facts which are challenging stay at the front of the box where they get daily practice. Facts which are mastered easily move quickly through the box. Sometimes a fact seems to be going well, but when it gets to fortnightly repetition, it becomes a struggle, and we realise it needs more review and practice.
If a fact is answered correctly, confidently and immediately from the final ‘Dates’ section, then I take it out of the box as being mastered.
What speed of recall should you require?
This is entirely up to you. People often say 2-3 seconds for maths facts. My child has a slower processing speed than average, so I generally allow 4 seconds at the front of the box, where we are really working on building visualisation strategies. However I won’t move a fact out of the final section of the box unless my child can answer confidently in under 2 seconds, which indicates (usually!) that they have mastered the skill of retrieving that fact quickly..
How do you decide when to add new facts to the box?
I try to have 3-5 new facts in the ‘several times daily’ section of the box. If there are too many cards in the box, it can become overwhelming. Occasionally I have needed to take some cards out because it was clearly too many and we were struggling to keep on top of them.

How do you decide the order for adding new facts?
Our order so far has been :
- Addition facts to 10
- Addition facts to 20
- Subtraction facts to 10
- Subtraction facts 20 (with 2x and 10x multiplication tables interspersed for some light relief! Those teen subtraction facts are challenging.)
Strategies within 10
For maths facts within 10, we made extensive use of the dice dot strategies in Ronit Bird’s e-book Exploring Numbers through Dot Patterns. I have written a review of Ronit Bird’s resources for dyscalculia here. These strategies helped us to make good progress through all facts up to 6, and the doubles and near-doubles facts up to 10.

Some of the other fact families such as 3+6=9 and 5+3=8 have proved more challenging and required more review. Ronit Bird has a number of games for these facts, and we have experimented with different visualisation strategies.
Strategies within 20
For addition facts within 20, we worked with the doubles facts first. One idea which was quite helpful was to use a mirror next to a ten frame to help with visualising doubles. (E.g. you put 7 counters on a ten frame, and then hold up a mirror next to it to see the double. This makes it clearer that it is 10+4 counters). The doubles facts helped a lot with close facts. For example, my child is absolutely solid that 6+6=12, so with lots of practice they can use that as a base for 6+7=13.
We also used some of the ten-frame strategies in Kate Snow’s Math with Confidence curriculum for Grade 1 and Grade 2. In particular, the idea of visualising ‘moving one counter’ from the bottom frame to the top frame for +9 facts was very helpful. Again, we needed to practice it quite a lot with manipulatives to then be able to use it mentally.

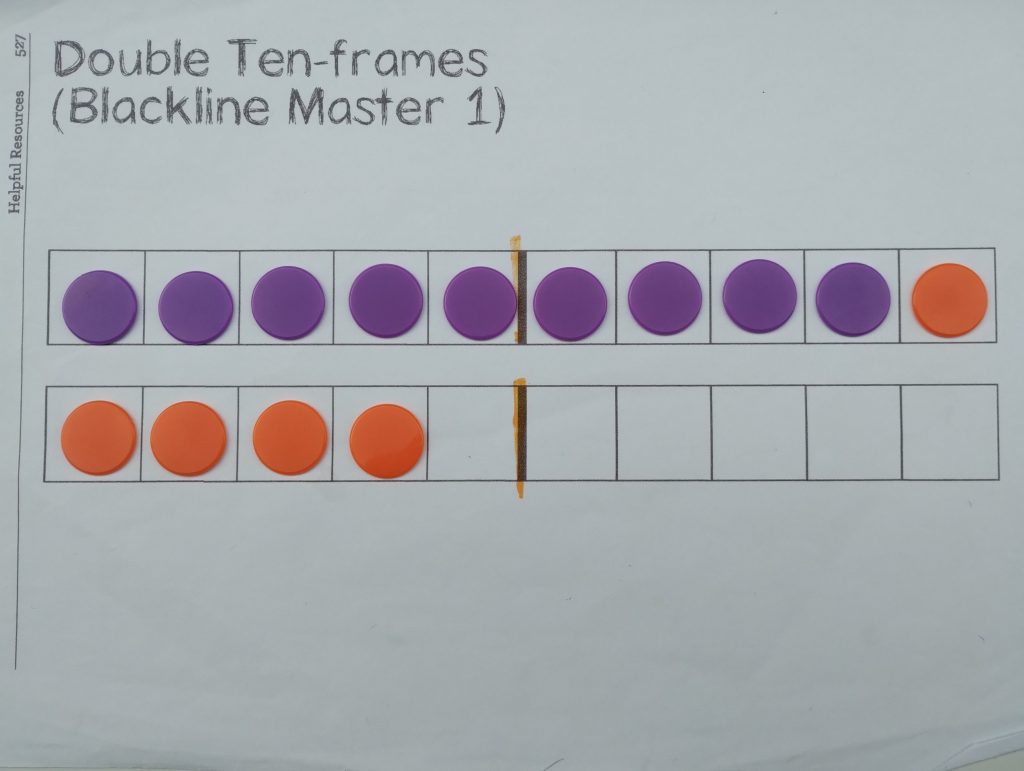
Subtraction facts within 20 have proven harder to learn, which is to be expected. For some facts, using a ‘parts-total mat’ strategy approach works well. This is another idea from Math with Confidence, thinking about fact families as two ‘parts’ joined by a ‘total’ above them. It helps that our flashcards are arranged in column form, so my child likes to visualise the missing ‘part’ as being roughly where the minus sign is.

The ten-frame also helps for some of these subtraction facts, especially those where the answer is 9. For 12-3, we can visualise taking two counters off the bottom frame, and then we only need to remove one more.
Strategies for multiplication
For the multiplication facts, I ask before each session: “What do we need to remember about multiplication?” The answer is “Groups!” This one word really helps my child to stay on task and not be tempted to add rather than multiply.
We have been trialling the Multiplication by Heart flashcards from Math for Love. This was because my usual Magic Scholar flashcards were no longer available, but I actually really like the Multiplication by Heart set. It uses different visualisation strategies on the flashcards to help kids really understand what multiplication is. My child has found the Cuisenaire rod-style array visualisation the most helpful, as they are already familiar with using the rods in other way.

So far we have only done the 10x and 2x times tables. We had some initial teething issues with understanding what multiplication is (e.g. a tendency to say 10 x 9 = 19) but having resolved those, these tables have been pretty plain sailing. My child is already confident on their doubles facts to 20 from adding. I will try to report back here when we’ve moved on to some harder tables!
Potential problems
Here are a few problems that have cropped up for us along the way.
Addition & subtraction confusion
After learning all the addition facts within 10, I tried to move on to the matching subtraction facts. This was a mistake for us! At this point my child was not totally rock solid on the concept of subtraction, and was tempted to do addition instead. They were really frustrated by getting facts wrong as a result, and it just wasn’t productive for us at that point in time. I tried saying before each question ‘this is a taking away one!’ but it wasn’t helping. We were moving backwards rather than forwards! Time to make changes.
I ended up taking all the subtraction facts out of the box, consolidating the addition to 10, and then moving onto addition to 20. That felt scary and big! But it was actually much less intimidating to my child than I expected, especially starting with +9 facts in line with our Math with Confidence math curriculum.
About half way through the addition to 20 facts, I was able to start adding in some easy subtraction facts within 10, and it went absolutely fine. I think those extra few months of maths practice had enabled my child to straighten out addition and subtraction conceptually, and they had almost no further problems with it.
Having too many facts
We have had a couple of points where we have been moving along nicely, everything going in the right direction, and then WHAM! My child starts to get more and more things wrong, the ‘daily’ section at the front of the box fills up, and suddenly maths fact practice feels long and painful. I have learned that this means I have put too much into the box. My child isn’t getting enough time to consolidate the facts they already have. It is time to take 5-10 cards out of the box and postpone them, which feels like going backwards, but it unlocks progress and a positive feeling of success at maths.
Facts that get missed for weekends
We don’t practice our facts at the weekend, so if a fact was in a date section that fell at a weekend (e.g. Saturday 3rd), it wouldn’t get practiced that week. For more consistency, I now go over the weekend’s facts on the Monday (e.g. we would do the 3rd, 4th and 5th sections on Monday morning).
Choosing flashcards
This post contains affiliate links. As an Amazon Associate, I earn from qualifying purchases.
I chose flashcards with the equation shown on the front, and the same equation with the answer included on the back. Our set of cards has a ‘column’ equation format. This has turned out to be really useful for subtraction, where my child often uses a ‘parts-total’ strategy from Math with Confidence. The column format makes it easier to visualise the missing addend.
Our flashcards are also colour coded. Green is addition, and blue is subtraction. This has been a helpful feature as we are now working on both categories at the same time.

The addition and subtraction flashcards that we use are Magic Scholar Flash Cards, but unfortunately they don’t seem to be easily available any more. You can the original listing at Amazon here:
The Think Tank Scholar flashcards are probably the most similar thing I have seen at present, although they are quite expensive, and seem to use a different colour coding scheme. You could of course make your own flashcards!
For multiplication, as the Magic Scholar cards were no longer available, I decided to try out the Math for Love: Multiplication by Heart cards. They were on the more expensive side, but I have been very pleased with them.

My child had very little previous exposure to multiplication, and was tempted to resort to adding (the symbols look very similar!). These cards, particularly the cards with array illustrations, have really helped to straighten things out. We remind ourselves each time that we need to think about ‘groups’. I don’t use the original box, I just slot them into our existing index card system, but they do come with their own spaced repetition system if you would prefer to use that. One comment I would make is that the array pictures look rather like Cuisenaire rods, which we often use. However, the colours are NOT the same as Cuisenaire rods, which initially confused my child a little.

We use this index card box and set of dividers, which has held up really well to a year of usage, and still looks in great condition.
If you are interested in finding out more about Ronit Bird’s resources for dyscalculic children, you might find it helpful to take a look at my review of her e-books.